Number Systems
TYPES OF NUMBER SYSTEMS
In the world of electronics math is very important. In order to know how to calculate voltage, current, power, resistance, and much more you must be able to use different types of math.
In these tutorials we will cover the basics that will help to introduce you to numbering systems that will help you in your future electronics projects.
Until now, you have probably used only one system, the decimal system. You may also be familiar with the Roman numeral system, even though you seldom use it.
THE DECIMAL NUMBER SYSTEM
In this section you will be studying modern systems. You should realize that these systems have certain things in common. These common terms will be defined using the decimal system as our base. Each term will be related to each system as that system is introduced.
Each of the number systems you will study is built around the following components: the UNIT, NUMBER, and BASE (RADIX).
Unit and Number
The terms unit and number when used with the decimal system are almost self-explanatory. By definition the unit is a single object; that is, an apple, a dollar, a day. A number is a symbol representing a unit or a quantity. The figures 0, 1, 2, and 3 through 9 are the symbols used in the decimal system. Thesesymbols are called Arabic numerals or figures. Other symbols may be used for different systems.
For example, the symbols used with the Roman numeral system are letters - V is the symbol for 5, X for 10, M for 1,000, and so forth. We will use Arabic numerals and letters in the number system discussions in this section.
Base (Radix)
The base, or radix, of a number system tells you the number of symbols used in that system. The base of any system is always expressed in decimal numbers. The base, or radix, of the decimal system is 10. This means there are 10 symbols - 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9 - used in the system.
A system using three symbols - 0, 1, and 2 - would be base 3; four symbols would be base 4; and so forth. Remember to count the zero or the symbol used for zero when determining the number of symbols used in a system.
The base of a number system is indicated by a subscript (decimal number) following the value of the number. The following are examples of numerical values in different bases with the subscript to indicate the base:
7592 base 10
214 base 5
123 base 4
656 base 7
You should notice the highest value symbol used in a number system is always one less than the base of the system. In base 10 the largest value symbol possible is 9; in base 5 it is 4; in base 3 it is 2.
Positional Notation and Zero
You must observe two principles when counting or writing quantities or numerical values. They are the POSITIONAL NOTATION and the ZERO principles.
Positional notation is a system where
the value of a number is defined not only by the symbol but by the
symbol’s position. Let’s examine the decimal (base 10) value of 427.5.
You may know from experience that this value is four hundred
twenty-seven and one-half. Now examine the position of each number:
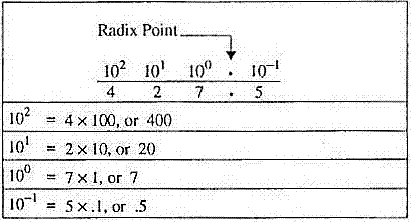
If 427.5 is the quantity you wish to express, then
each number must be in the position shown. If you exchange the positions
of the 2 and the 7, then you change the value.
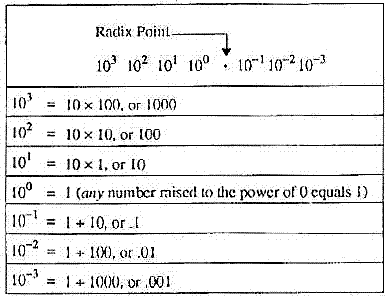
You can see that the power of the base is multiplied by the number in
that position to determine the value for that position.The following
graph illustrates the progression of powers of 10:
All numbers to the left of the decimal point are whole numbers, and all numbers to the right of the decimal point are fractional numbers. A whole number is a symbol that represents one, or more, complete objects, such as one apple or $5. A fractional number is a symbol that represents a portion of an object,such as half of an apple (.5 apples) or a quarter of a dollar ($0.25). A mixed number represents one, or more, complete objects, and some portion of an object, such as one and a half apples (1.5 apples).
When you use any base other than the decimal system, the division between whole numbers and fractional numbers is referred to as the RADIX POINT. The decimal point is actually the radix point of the decimal system, but the term radix point is normally not used with the base 10 number system.
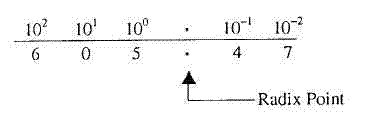
Just as important as positional notation is the use of the zero. The placement of the zero in a number can have quite an effect on the value being represented. Sometimes a position in a number does not have a value between 1 and 9. Consider how this would affect your next paycheck.
If you were expecting a check for $605.47, you wouldn’t want it to be $65.47. Leaving out the zero in this case means a difference of $540.00. In the number 605.47, the zero indicates that there are no tens. If you place this value on a bar graph, you will see that there are no multiples of 101.
Most Significant Digit and Least Significant Digit (MSD and LSD)
Other important factors of number systems that you should recognize are the MOST SIGNIFICANT DIGIT (MSD) and the LEAST SIGNIFICANT DIGIT (LSD).
The MSD in a number is the digit that has the greatest effect on that number.
The LSD in a number is the digit that has the least effect on that number.
Look at the following examples:
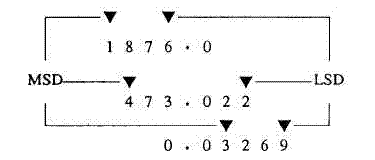
You can easily see that a change in the MSD will increase or decrease the value of the number the greatest amount. Changes in the LSD will have the smallest effect on the value.
The
nonzero digit of a number that is the farthest LEFT is the MSD, and the
nonzero digit farthest RIGHT is the LSD, as in the following example:
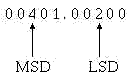
In a whole number the LSD will always be the digit immediately to the left of the radix point.
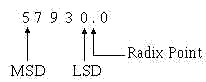
Carry and Borrow Principles
Binary Number Systems
MSD and LSD
Binary Addition
Binary Addition Continued
Binary Subtraction
Complimentary Subtraction
Complimentary Subtraction Continued
Octal
Octal Number Addition
Octal Number Subtraction
Hexadecimal
Hex Number Addition
Hex Number Subtraction
Conversion of Bases
Base Conversions Continued
Decimal to Octal
Decimal to Hex
Binary Conversion
Binary to Hex, Hex to Binary, and Octal to Hex
Octal Conversion
Hex to Decimal
Binary Coded Decimal















